步进电机驱动方式的分类及比较:步进电机驱动方法的分类主要有恒电压驱动方式、恒电流斩波驱动方式和细分驱动方式。以下是这几种驱动方式的简介及比较。
1 恒电压驱动方式
1.1 单电压驱动 单电压驱动是指在电机绕组工作过程中,只用一个方向电压对绕组供电。如图所示,L为电机绕组,VCC为电源。当输入信号In为高电平时,提供足够大的基极电流使三极管T处于饱和状态,若忽略其饱和压降,则电源电压全部作用在电机绕组上。当In为低电平时,三极管截止,绕组无电流通过。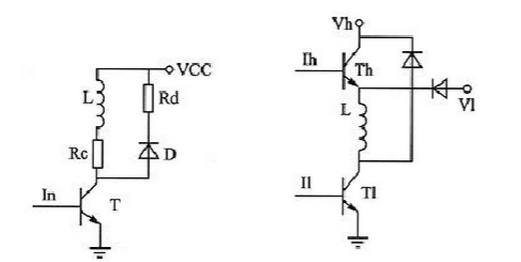
为使通电时绕组电流迅速达到预设电流,串入电阻Rc;为防止关断T时绕组电流变化率太大,而产生很大的反电势将T击穿,在绕组的两端并联一个二极管D和电阻Rd,为绕组电流提供一个泄放回路,也称“续流回路”。
单电压功率驱动电路的优点是电路结构简单、元件少、成本低、可靠性高。但是由于串入电阻后,功耗加大,整个功率驱动电路的效率较低,仅适合于驱动小功率步进电机。
1.2 高低压驱动 为了使通电时绕组能迅速到达设定电流,关断时绕组电流迅速衰减为零,同时又具有较高的效率,出现了高低压驱动方式。如上图所示,Th、T1分别为高压管和低压管,Vh、V1分别为高低压电源,Ih、I1分别为高低端的脉冲信号。在导通前沿用高电压供电来提高电流的前沿上升率,而在前沿过后用低电压来维持绕组的电流。高低压驱动可获得较好的高频特性,但是由于高压管的导通时间不变,在低频时,绕组获得了过多的能量,容易引起振荡。可通过改变其高压管导通时间来解决低频振荡问题,然而其控制电路较单电压复杂,可靠性降低,一旦高压管失控,将会因电流太大损坏电机。
2 恒电流斩波驱动方式
2.1 自激式恒电流斩波驱动 图为自激式恒电流斩波驱动框图。把步进电机绕组电流值转化为一定比例的电压,与D/A转换器输出的预设值进行比较,控制功率管的开关,从而达到控制绕组相电流的目的。从理论上讲,自激式恒电流斩波驱动可以将电机绕组的电流控制在某一恒定值。但由于斩波频率是可变的,会使绕组激起很高的浪涌电压,因而对控制电路产生很大的干扰,容易产生振荡,可靠性大大降低。
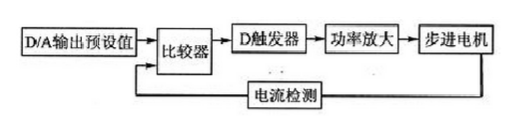
2.2 它激式恒电流斩波驱动 为了解决自激式斩波频率可变引起的浪涌电压问题,可在D触发器加一个固定频率的时钟。这样基本上能解决振荡问题,但仍然存在一些问题。比如:当比较器输出的导通脉冲刚好介于D触发器的2个时钟上升沿之间时,该控制信号将丢失,一般可通过加大D触发器时钟频率解决。
3 细分驱动方式 这是本文讨论的重点,也是该系统采用的驱动方法。细分驱动最主要的优点是步距角变小,分辨率提高,且提高了电机的定位精度、启动性能和高频输出转矩;其次,减弱或消除了步进电机的低频振动,降低了步进电机在共振区工作的几率。可以说细分驱动技术是步进电动机驱动与控制技术的一个飞跃。 细分驱动是指在每次脉冲切换时,不是将绕组的全部电流通入或切除,而是只改变相应绕组中电流的一部分,电动机的合成磁势也只旋转步距角的一部分。细分驱动时,绕组电流不是一个方波而是阶梯波,额定电流是台阶式的投入或切除。比如:电流分成n个台阶,转子则需要n次才转过一个步距角,即n细分, 如图所示。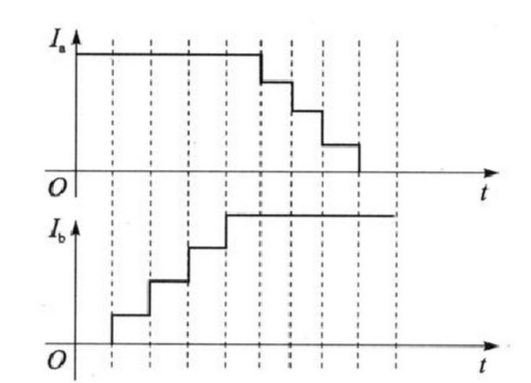
一般的细分方法只改变某一相的电流,另一相电流保持不变。如图5所示,在O°~45°,Ia保持不变,Ib由O逐级变大;在45°~90°,Ib保持不变,Ia由额定值逐级变为0。该方法的优点是控制较为简单,在硬件上容易实现;但由图6所示的电流矢量合成图可知,所合成的矢量幅值是不断变化的,输出力矩也跟着不断变化,从而引起滞后角的不断变化。当细分数很大、微步距角非常小时,滞后角变化的差值已大于所要求细分的微步距角,使得细分实际上失去了意义。
这就是目前常用的细分方法的缺陷,那么有没有一种方法让矢量角度变化时同时保持幅值不变呢?由上面分析可知,只改变单一相电流是不可能的,那么同时改变两相电流呢?即Ia、Ib以某一数学关系同时变化,保证变化过程中合成矢量幅值始终不变。基于此,本文建立一种“额定电流可调的等角度恒力矩细分”驱动方法,以消除力距不断变化引起滞后角的问题。如图所示,随着A、B两相相电流Ia、Ib的合成矢量角度不断变化,其幅值始终为圆的半径。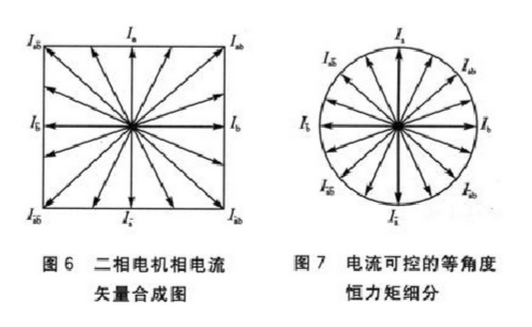
下面介绍合成矢量幅值保持不变的数学模型:当Ia=Im·cosx,Ib=Im·sinx时(式中Im为电流额定值,Ia、Ib为实际的相电流,x由细分数决定),其合成矢量始终为圆的半径,即恒力距。
等角度是指合成的力臂每次旋转的角度一样。额定电流可调是指可满足各种系列电机的要求。例如,86系列电机的额定电流为6~8 A,而57系列电机一般不超过6 A,驱动器有各种档位电流可供选择。细分为对额定电流的细分。
为实现“额定电流可调的等角度恒力距”,理论上只要各相相电流能够满足以上的数学模型即可。这就要求电流控制精度非常高,不然Ia、Ib所合成的矢量角将出现偏差,即各步步距角不等,细分也失去了意义。